到处都是坐标下降

Series: algo January 23, 2018

坐标下降是坐标下降

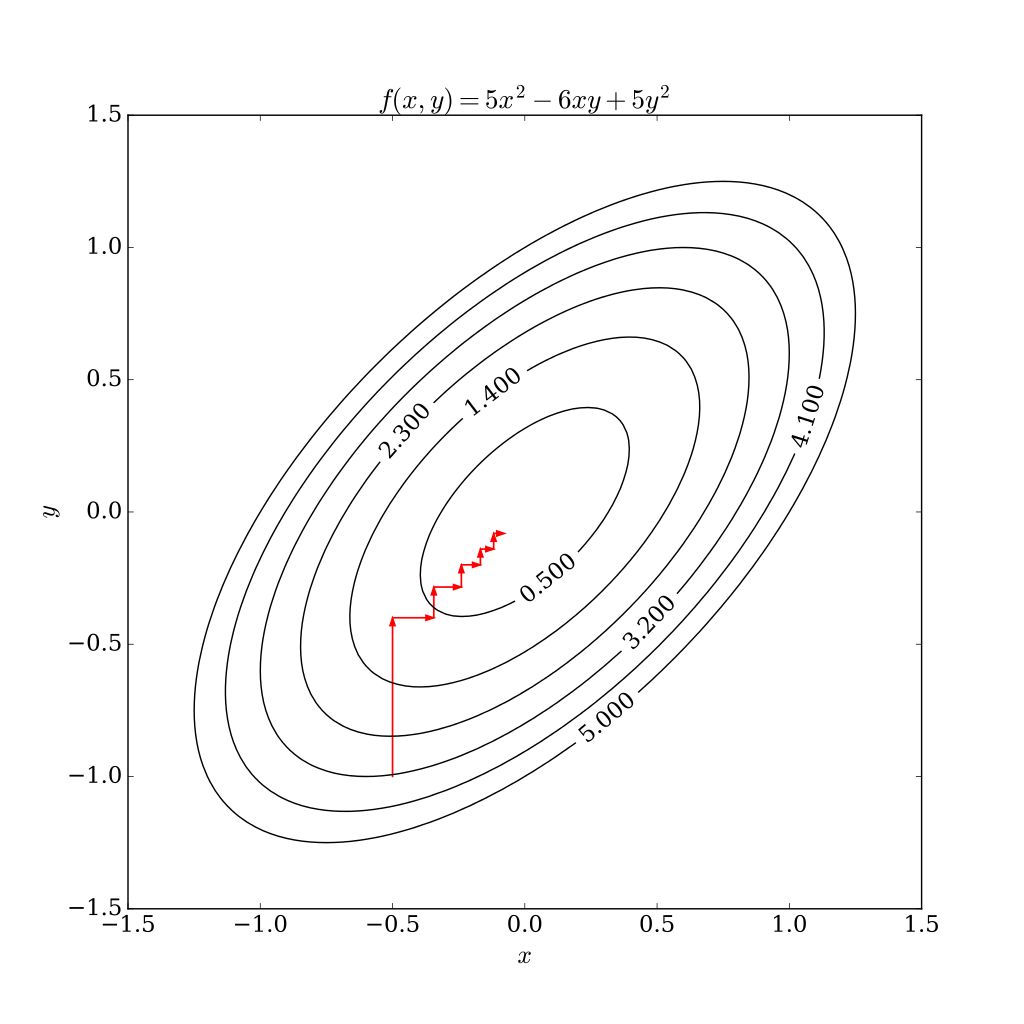
坐标下降法基于的思想是多变量函数F(x1, …, xn)可以通过每次沿一个方向优化来获取最小值，在整个过程中循环使用不同的坐标方向，直至函数收敛。

求解SVM对偶形式的SMO算法是坐标下降

带软间隔的SVM的优化问题最后可写为：

$max_\alpha W(\alpha)=\sum_{i=1}^{m} \alpha_i - {1 \over 2}\sum_{i,j=1}^{m} y^{(i)}y^{(j)} \alpha_i \alpha_j x^{(i)} x^{(j)} \\ s.t. 0 \leqslant \alpha_i \leqslant C, i = 1,...,m \\ \sum_{i=1}^{m}\alpha_iy^{(i)} = 0$

SMO算法给出的解法是每一步选取一对 $\alpha_i$ 和 $\alpha_j$，固定除 $\alpha_i$ 和 $\alpha_j$ 之外的其他参数，根据约束条件将 $\alpha_j$ 写为 $\alpha_i$ 的函数表示，并确定W极值条件下的 $\alpha_i$ 的取值。

SMO算法的每一步可被视为对 $\alpha_i$（及 $\alpha_j$ ）完成了一步坐标下降。

EM算法是坐标下降

对于存在可观测变量X，隐变量Z，及参数theta的模型，用于求解其参数极大似然估计的EM算法可写为最大化模型的free energy：

$F(q,\theta) = -D_{KL}(q||p_{Z|X}(-|x;\theta)) + logL(\theta;x)$

其中$q$为关于隐变量的一个概率分布，$D_{KL}$为两个分布的KL散度。

则EM算法可被视为$q$和$D_{KL}$间的坐标下降：

E-Step: $ q^{(t)} = argmax_q F(q, \theta^{(t)})$
M-Step: $ \theta^{(t+1)} = argmax_{\theta}F(q^{(t)}, \theta)$

(Mean Field) Variational Inference是坐标下降

Variational inference 尝试使用一个“简单”的概率分布$q(z_{1:m})$对后验概率分布$p(z_{1:m}|x)$进行近似。这一方法尝试优化的目标是最小化$q(z_{1:m})$与$p(z_{1:m}|X)$间的KL散度，亦等价于最大化模型的ELBO (evidence lower bound)。

Mean field variational inference中进一步假设$q(z_{1:m})$中各分量是独立的：

$q(z_{1:m}) = q(z_1)q(z_2)...q(z_m)$

Mean field variational inference采用迭代的方式进行求解。在每一步中，选取其中一个分量$q_k$，固定其余分量不变，通过改变$q_k$以最大化ELBO，不断迭代求解直至完成对后验概率的近似。

Mean field variational inference算法的每一步可被视为对$q_k$完成了一步坐标下降。

Gibbs Sampling(勉强)是坐标下降

在Gibbs Sampling中，算法以迭代的方式对联合分布中的每个分量进行采样。对于$x_j$的第i+1次迭代，算法从以下分布中采样得到新的样本：

$x_j \sim p(x_j^{(i+1)} | x_1^{(i+1)}, x_2^{(i+1)}, ..., x_{j-1}^{(i+1)}, x_{j+1}^{(i)}, ..., x_{n}^{(i)})$

这一逐个坐标进行采样的算法能够保证：

所采样本近似联合概率分布
样本的子集可用于近似边缘概率分布
各坐标的均值可近似各变量的期望

这一算法的每次迭代可以视作对目标分布的一次坐标逼近。

到处都是坐标下降

更广义的坐标下降：当原问题不易解时，将原问题划分为若干个更易解的子问题进行迭代求解，并证明迭代算法会收敛至原问题的解。